[정리] Time Series Deconfounder: Estimating Treatment Effects over Time in the Presence of Hidden Confounders (Ioana Bica, ICML 2020)

Author: Ioana Bica, Ahmed M Alaa, Mihaela van der Schaar
Paper Link: https://arxiv.org/abs/1902.00450

Talk in ICML2020: https://icml.cc/virtual/2020/poster/6131

Talk in van der Schaar Lab's Yutube Channel:  https://www.youtube.com/watch?v=TNPce1zd6rE 

Code: https://github.com/ioanabica/Time-Series-Deconfounder

 

 

0. Abstract

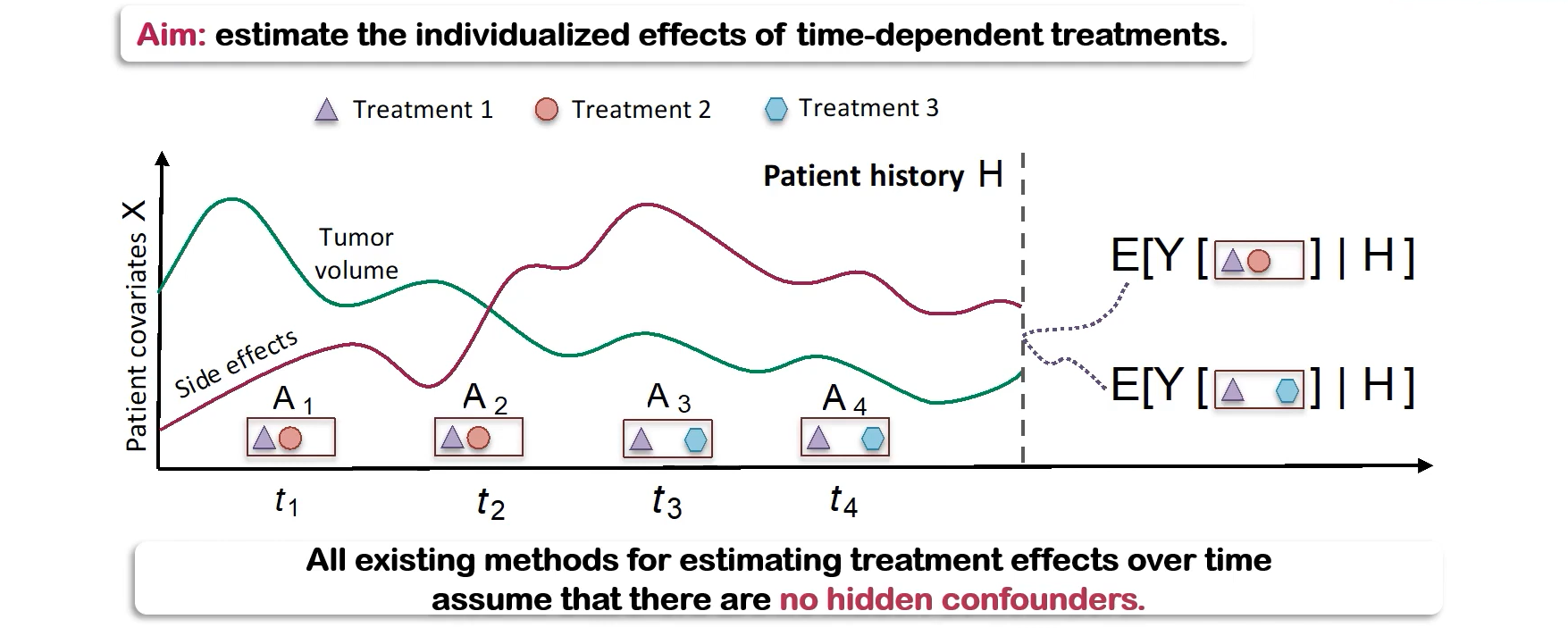
• 의료분야에서 treatment effect를 추론하는것은 중요하지만, 지금까지의 추론 방법들은 모두 'no hidden confounder'라는 비현실적이고 결과적으로 추론에 bias를 야기하는 가정을 전제로 함.
• 본 연구에서는 시간에 따른 다중 치료 환경에서 multi-cause hidden confounder가 존재할때의 treatment effect를 추론하기위한 Time Series Deconfounder를 제안함.
• Time series Decounfounder는 multitask output의 RNN을 factor model로 사용하여 multi-cause unobserved confounder를 대체하는 latent variable을 추론하고 이를통해 casual inference를 수행함.  
• 이론적 분석과 함께 시뮬레이션 및 실제 MIMIC III데이터를 사용하여 알고리즘의 효과성을 검증함.

1. Introduction

• 연속적으로 처방된 치료에 따른 환자 개인의 치료 효과를 예측하는것은 매우 중요한 문제임.
• 최근 이러한 정보를 담고있는 observational 데이터 역시 빠르게 증가하고 있음.
• 하지만 기존의 방법들은 모든 confounder가 관측가능하다는 대체로 비현실적인 상황을 가정하고있어 예측에 bias가 생김.
• 예를들어 암의 진행에대한 항암제의 효과를 예측할 때 환자의 약에대한 내성형성이나 누적되는 독성을 고려하지 않는것은 예측결과에 bias를 초래.
• 하지만 내성이나 독성은 관측이 어렵고 관측이 되더라고 후향적인 EHR과 같은 후향적인 관측데이터에는 기록되어있지 않은 경우가 대부분.
• 본 연구에선 Wang & Blei (2019a)의 연구에서 고안된 'static 셋팅에서의 multiple treatment를 활용하여 hidden confounder를 deconfounding하는 방법'을 개선하여 longitudinal 셋팅에서의 time-varying hidden confounder를 deconfounding하는 Time Series Deconfounder를 제안함.
• 시계열 환경에서 unobserved confounder의 대체재로서 letent variable을 학습하는 첫번째 시도.

 

2. Related Work

• 시간에 따라 변하는 치료에 대한 Potential outcomes
  - 지금까지 시계열 데이터에 대한 counterfacutal inference로는 G-formula, G-estimation, MSM, R-MSN, balaced representation 등이 있었지만 모두 hidden confounder가 없다고 가정.
  - 연속성 데이터에대한 treatment effect 연구들도 있어왔으나 여기선 이산 환경을 다룸.
  - Unmeasured confounder에 대한 potential impact를 평가하기위한 sensitivity anlysis방법들도 고안되어옴.
• Hidden confounder 추론을 위한 latent variable 모델
  - Multi-cause 환경에서 hidden confounder를 추론가능한 latent variable로 대체하고 추론된 latent variable로 causal inference를 수행하는식의 deconfounder 접근은  Wang & Blei (2019a, link)에서 제안된 바 있음.
  - 해당 논문은 static treatment 문제를 다루고 있으나, 본 논문은 이와 달리 time-varying treatment문제를 다루기 위해 RNN을 factor model로 사용하는 deconfounder 구조를 제안함. 

 

3. Problem Formulation

• $\mathbf{X}_{t}^{(i)} \in \mathcal{X}_{t}$: random variable, (환자 $i$에 대한; 이후 생략) time-dependent covariates
• $\mathbf{A}_{t}^{(i)}=\left[A_{t1}^{(i)}{\cdots}A_{tk}^{(i)}\right]\in\mathcal{A}_{t}$: 시간 $t$에서의 가능한 $k$가지 treatments
• $\mathbf{Y}_{t+1}^{(i)}\in\mathcal{Y}_{t}$: 관측된 outcomes
• $\tau^{(i)}=\left\{{\mathbf{x}_t^{(i)}},{\mathbf{a}_t^{(i)}},{\mathbf{y}_{t+1}^{(i)}}\right\}_{t=1}^{T^{(i)}}$: 이산시간 $T^{(i)}$ 동안 수집된 trajectory 샘플
• $\mathcal{D}=\left\{{\tau^{(i)}}\right\}_{i=1}^{N}$: $N$명의 환자에 대한 EHR 데이터
• $\overline{\mathbf{A}}_t=(\mathbf{A}_1,\cdots,\mathbf{A}_t)\in\overline{\mathcal{A}}_t$: 시간 $t$까지의 treatment history
• $\overline{\mathbf{X}}_t=(\mathbf{X}_1,\cdots,\mathbf{X}_t)\in\overline{\mathcal{X}}_t$: 시간 $t$까지의 covariates history
• $\mathbf{Y}(\overline{a})$: 가능한 treatment course $\overline{a}$에 대한 potential outcome (factual & counterfactual)
• 아래의 Individualized treatment effect (ITE), 즉 환자 개인의 covariate history와 treatment history가 주어졌을때의 potential outcome, 을 추론하는것이 이 연구의 목표

$\mathbb{E}[\mathbf{Y}(\overline{a}_{\geq{t}}){\vert}\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]$

• 아래 세 가지 가정 하에서는 bias가 생기지 않아 위 potential outcome에 대한 추론은 우항의 관측된 outcome에 대한 regression과 동치

 $\mathbb{E}[\mathbf{Y}(\overline{a}_{\geq{t}}){\vert}\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]=\mathbb{E}[\mathbf{Y}{\vert}\overline{a}_{\geq{t}},\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]$

  Assumption 1. Consistency

  Assumption 2. Positivity (Overlap)

  Assumption 3. Sequencial strong ignorability (no hidden confounders)

$\mathbf{Y}(\overline{a}_{\geq{t}}){\perp\!\!\!\!\perp}\mathbf{A}_t\vert\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_{t}$

• 하지만 세번째 가정은 좌변의 counterfactual로 인해 테스트가 불가능하며 현실적이지 않아 여기서는 hidden confounder가 있는 보다 현실적인 문제를 다루고자 함.
• 따라서 위에서 언급한 동치는 성립하지 않음.

$\mathbb{E}[\mathbf{Y}(\overline{a}_{\geq{t}}){\vert}\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]\neq \mathbb{E}[\mathbf{Y}{\vert}\overline{a}_{\geq{t}},\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]$

• 대신 Wang & Blei (2019a)의 접근을 확장하여 시간에 따른 다중 treatments를 활용한 sequencial latent variable $\overline{\mathbf{Z}}_t=(\mathbf{Z}_1,\cdots,\mathbf{Z}_t)\in\overline{\mathcal{Z}}_t$ 을 추론하고 관측되지 않은 confounders로서 대체하고자 함.

 

4. Time Serise Deconfounder

• 본 연구에서 제안하는 Time Series Deconfounder의 본질적인 아이디어는 multi-cause confounder로 인한 treatment들 사이의 종속성이 있다는것.
• 이 종속성을 활용하여 시간에 따라 바뀌는 treatment로 부터 hidden confounder를 추론함.

4.1. Factor Model

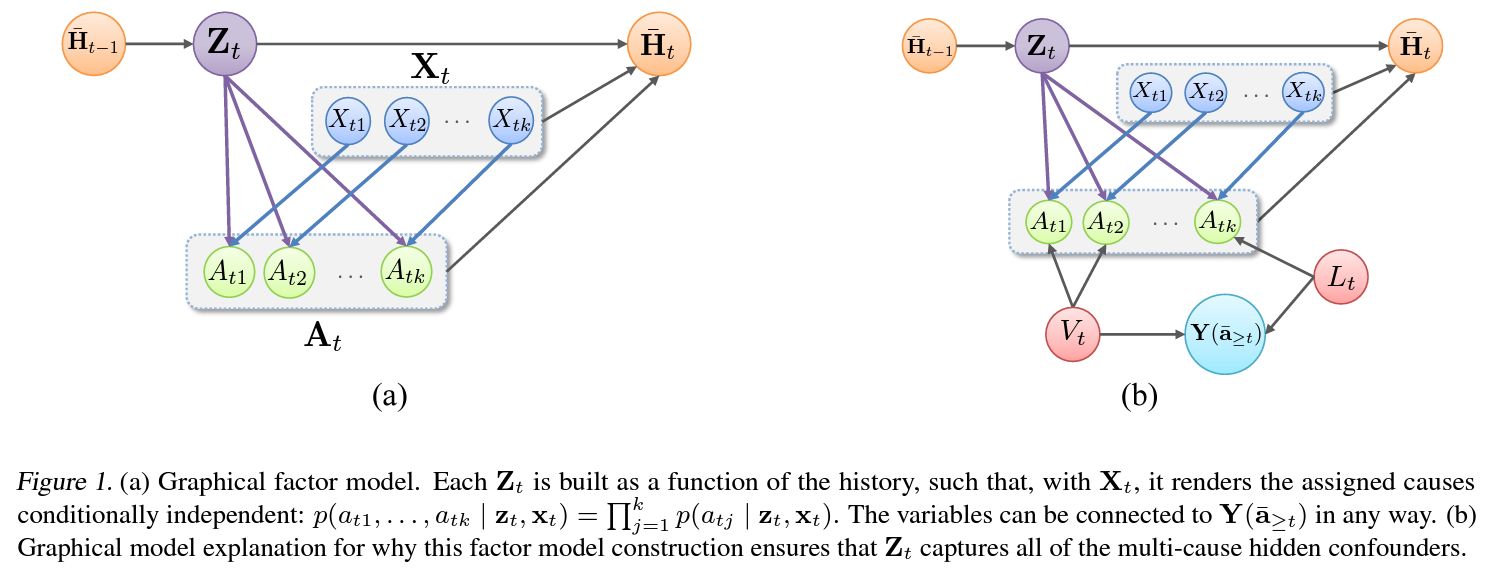
• Time Series Deconfounder는 시간 $t$이전까지의 history $\overline{\mathbf{h}}_{t-1}$로부터 시간 $t$에서의 unobserved confounder를 대체할  letent variable $z_t$을 추론하는 factor model $g$을 가짐.

$\mathbf{z}_t=g(\overline{\mathbf{h}}_{t-1})$

,where  $\overline{\mathbf{h}}_{t-1}=(\overline{\mathbf{a}}_{t-1},\overline{\mathbf{x}}_{t-1},\overline{\mathbf{z}}_{t-1})$

• 이를 그래프로 나타내면 위 그림$(a)$와 같으며, latent variable  $\mathbf{z}_t$는 시간 $t$에서의 treatment들에 대한 multi-cause unobserved confounder를 대체하는 역할로서 나타낼 수 있음. 
• Multi-cause unobserved confounder로 인한 treatment들 사이의 종속성으로 인해 factor model을 사용하여 latent variable의 sequence $\overline{\mathbf{Z}}_t$를 추론 할 수 있음.
• 이때, latent variable $\mathbf{Z}_t$는 모든 multi-cause confounder를 내포하고 있음을 보장 (treatment사이의 종속성을 활용한 귀류법).
• 즉, 위 그림$(b)$에서와 같이 또다른 multi-cause confounder $V_t$는 존재하지 않음.
• 하지만 $L_t$와 같은 single-cause confounder가 없는것은 보장할 수 없으므로 다음을 새롭게 가정하고, 위에서 언급한 기존 방법들에서 사용한 세가지 가정 중 세번째 가정을 대체.

  Assumption 3. Sequential single strong ignorability (no hidden single cause confounders)

$\mathbf{Y}(\overline{a}_{\geq{t}}){\perp\!\!\!\!\perp}{A}_{tj}\vert\mathbf{X}_{t},\overline{\mathbf{H}}_{t-1}$

• 물론 이 가정 역시 여전히 테스트가 불가능하지만, 관측가능한 treatment의 갯수가 증가함에 따라 hidden confounder가 하나의 treatment에만 영향을 줄 가능성은 급격히 줄어듬.
• Wang & Blei (2019a)에 따르면 $\mathbf{Z}_t$의 차원이 treatments의 갯수보다 작을경우 가정2. Positivity또한 실질적으로 만족가능.
• Fitting된 factor model이 얼마나 정확하게 validation set 환자의 treatment분포를 예측하는지를 평가하기위해 predictive check로서 각 시간 $t$에서 $M$개의 예측 샘플과 실제treatment 사이의 $p$-value를 아래와 같이 계산.

$\frac{1}{M}\sum_{i=1}^{M}\mathbf{1}(T(a_{t,rep}^{i})<T(a_{t,val}))$

,where $T(a_t)=\mathbb{E}_z[\mathrm{log}\,p(a_t{\vert}Z_t,X_t)]$ is test statistic and $\mathbf{1(\cdot)}$ is indicator function

• Fitting이 잘 된 경우 $p$-value는 0.5에 가까움.

4.2. Outcome Model

• Factor model이 잘 fitting된 다음 스텝으로 Time Series Deconfounder는 아래의 좌변의 시간에 따른 individualized treatment effect를 추론하기위한 outcome model을 우변과 같이 fitting.

$\mathbb{E}[\mathbf{Y}(\overline{a}_{\geq{t}}){\vert}\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]=\mathbb{E}[\mathbf{Y}{\vert}\overline{a}_{\geq{t}},\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]$

• Time Series Deconfounder의 uncertainty는 factor model에서 시간에 따라 샘플된 sequential latent variable $\hat{\bar{\mathbf{Z}}}_t=(\hat{\mathbf{Z}}_1,\cdots,\hat{\mathbf{Z}}_t)$ 을 다시 반복 샘플하여 구한 각각의 outcome들의 variance로 판단함.
• 만약 treatment effect가 부정확하여 non-identifiable할 경우엔 이 variance가 커짐.
• 또한 본 연구에서 제안하는 hidden confounder문제를 다루기 위해 latent variable를 추론하는 접근은 treatment effect의 bias를 명백히 낮추지만, Wang & Blei (2019a)에 따르면 hidden confounder가 없는 상황에선 기존 방법 대비 variance가 상대적으로 커져 free lunch는 아님. 

 

5. Factor Model over Time in Practice

• 시계열 문제를 다루고 있으므로 기존의 PCA나 Deep Exponential Families을 사용하는 대신 아래 그림과 같이 RNN, 여기서는 특히 LSTM을 factor model로서 사용함.

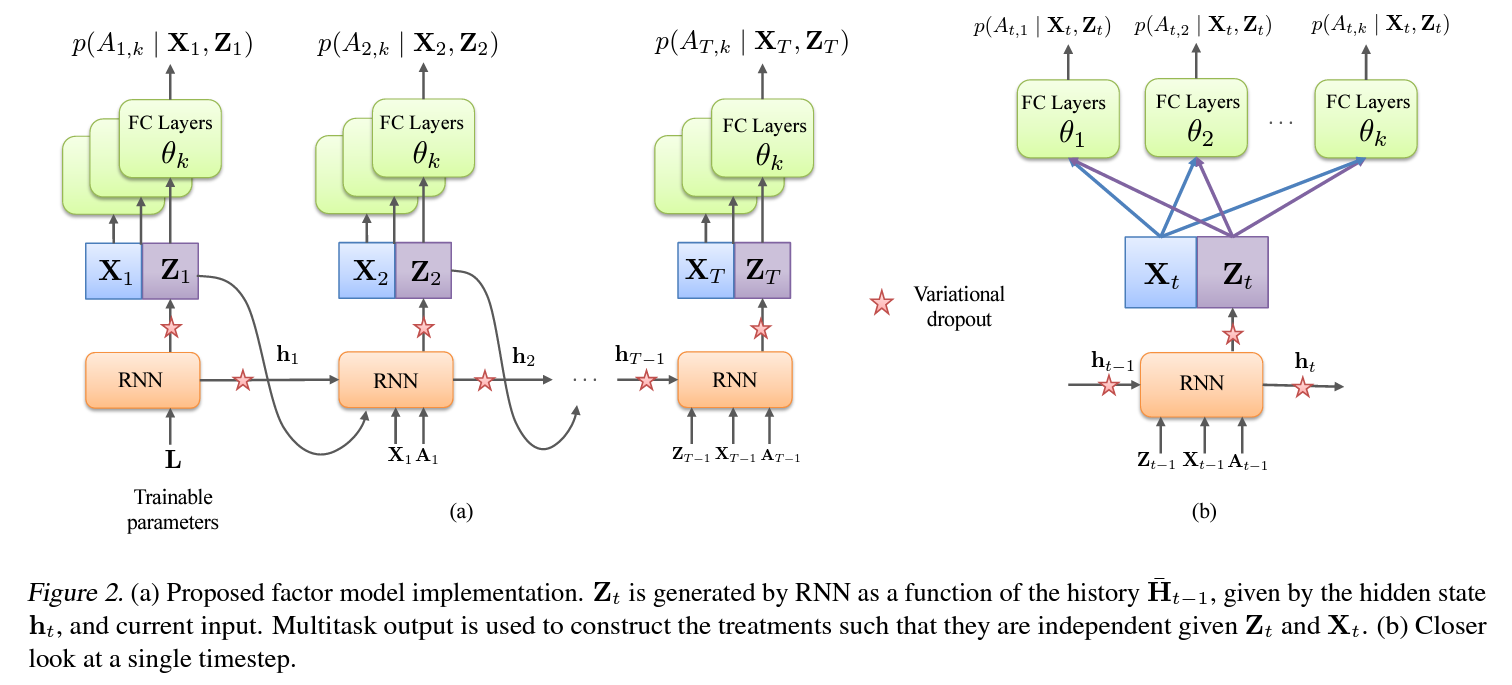
• 즉, RNN을 사용하여 환자의 시간 $t$까지의 history로 부터 시간 $t$에서의 latent variable을 추론.

$\mathbf{Z}_1=\mathrm{RNN}(\mathbf{L})$

$\mathbf{Z}_t=\mathrm{RNN}(\overline{\mathbf{Z}}_{t-1},\overline{\mathbf{X}}_{t-1},\overline{\mathbf{A}}_{t-1},\mathbf{L})$

• RNN의 출력사이즈는 $D_Z$이며 $\mathbf{L}$은 학습가능한 initial paramter.
• RNN에서 추론된 Latent variables $\mathbf{Z}_t$와 관측된 covariates $\mathbf{X}_t$에 조건부 독립인 treatment $\mathbf{A}_t=[A_{t1},\cdots,A_{tk}]$를 추론하기위해서 treatment 개수 $k$만큼의 single FC MLP레이어를 RNN의 출력단에 multitask output으로 붙임.

$A_{tj}=\mathrm{FC}(\mathbf{X}_t, \mathbf{Z}_t;\theta_j)$

• Binary treatment의 경우엔 출력레이어에 sigmoid activation을 사용함.
• Factor model의 확률적인 특징을 구현하기위해서 위 그림의 별이 그려진 부분에 $variational\,dropout$(GAL & Ghahramani, 2016a)을 사용하였고, 이에 따른 latent variable의 샘플링이 가능해짐.
• 위와 같은 구현으로 RNN으로 하여금 $\overline{\mathbf{X}}_t$, $\overline{\mathbf{Z}}_t$ 및 $\overline{\mathbf{A}}_t$사이의 복잡환 관계를 학습도록 할 수 있지만, 이 과정에서 predictive check가 반드시 필요하다는것에 주의.

 

6. Experiments on Synthetic Data

• 제안한 Time Series Deconfounder를 검증하고자 합성데이터를 사용함.
• 실제 데이터를 사용한 검증은 hidden confounder를 알 수 없으므로 불가능.

6.1. Simulated Dataset

• 5000명의 환자에 대한 20~30 스텝의 가상데이터를 treatments, covariates, hidden confounders가 서로 영향을 미치는 $p$-order autoregressive 과정으로 생성함 (자세한 수식은 논문 참조).
• 그리고 outcome은 covariates와 hidden confounder의 함수가 되도록 생성.

6.2. Evaluating Factor Model using Predictive Checks

• 제안한 factor model 아키텍처가 treatment의 분포를 잘 학습하는지 확인하고자 합성데이터에 대해 아래 세 가지 모델의 predictive check를 수행함.
  1. 제안한 factor model; RNN + Multitask FC output (초록)
  2. RNN대신 MLP를 사용한 factor model (파랑)
  3. Multitask FC layer대신 단일 FC layer를 사용한 factor model (보라)

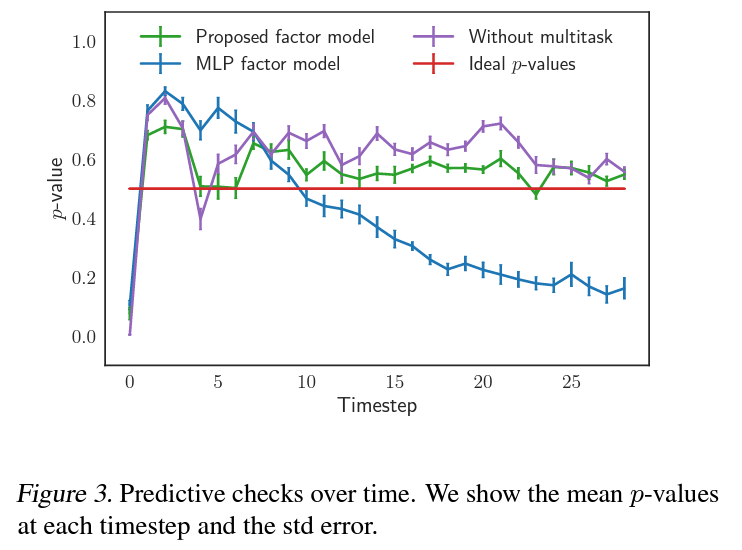
• 실험 결과 RNN대신 MLP를 사용할 경우 시간이 지남에 따라 지속적인 distribution mismatch가 생김.
• Multitask output은 treatment distribution을 파악하는데 도움은 되나 큰 영향을 주는것은 아님을 확인.
• 즉, factor model에 RNN아키텍처를 사용하는것이 hidden confounder의 시간 의존적인 특성을 캡쳐하는데 있어 중요하며, 현재 스텝의 covariates와 confounders가 잘 명시될 경우 treatment distribution을 학습할 수 있다고 결론.

6.3. Deconfounding the Estimation of Treatment Responses over Time

• Time Series Deconfounder가 confounder에 의한 bias를 잘 deconfounding하는지를 다음의 두 outcome model을 사용하여 검증함. 

1. Standard Marginal Structural Models (MSMs)
   - Logistic regression으로 구한 inverse probability of treatment weighting(IPTW)을 사용하여 confounder가 balance된 pseudo-population을 생성하는 단계와, 이렇게 생성된 pseudo-population으로부터 treatment reponse를 linear regression하는 단계의 두 가지 스텝으로 구성된 selection bias 대응방법.
   - 이름에서 'marginal'은 counfounder control의 의미이며, 'structural'은 potential outcome framework를 의미함.
   - MSMs에 대한 자세한 내용은 다음 두 강의를 참고
   (https://www.youtube.com/watch?v=7NjIQTzADgQ)
   (https://www.coursera.org/lecture/crash-course-in-causality/marginal-structural-models-EUpei)
2. Recurrent Marginal Structural Networks (R-MSNs; Lim et al., 2018)
   - MSMs와 접근은 같지만 RNN을 사용하여 propensity score를 추론하고 treatment response 역시 RNN을 사용하여 추론하는것이 차이.
   - $\mathrm{RNN}(\overline{\mathbf{X}}_t,\overline{\mathbf{Z}}_t,\overline{\mathbf{A}}_t)$ 와 같이 구현하며, RNN을 사용하여 추정한 propensity weights에 따라 weight를 각 환자에 주어 loss함수를 계산.

• 평가를 위해 한 스텝 다음의 treatment response를 예측하는 테스크를 사용하였으며, 두 outcome model에 대한 자세한 분석을 위해 아래 5가지 경우를 비교
  1) Confounded: hidden confounder를 고려하지 않고 관측데이터를 그대로 사용한 경우. 
  2) Deconfounded ($D_z=1$): 실제 hidden confounder의 크기인 1과 동일한 크기의 latent variable $\hat{\overline{\mathbf{Z}}}_t$를 사용한 경우.
  3) Deconfounded ($D_z=5$): 실제 hidden confounder의 크기인 1과 다른, 크기 5의 latent variable $\hat{\overline{\mathbf{Z}}}_t$를 사용한 경우.
  4) Deconfounded w/o $X_1$: Assumption 3를 위반한 경우로 single cause confounder $X_1$를 covariate에서 제거하여 hidden confounder로 가정한 경우.
  5) Oracle: 합성데이터에서의 실제 ground truth hidden confounder $\overline{\mathbf{Z}}_t$를 outcome 모델에 넣어준 경우. 

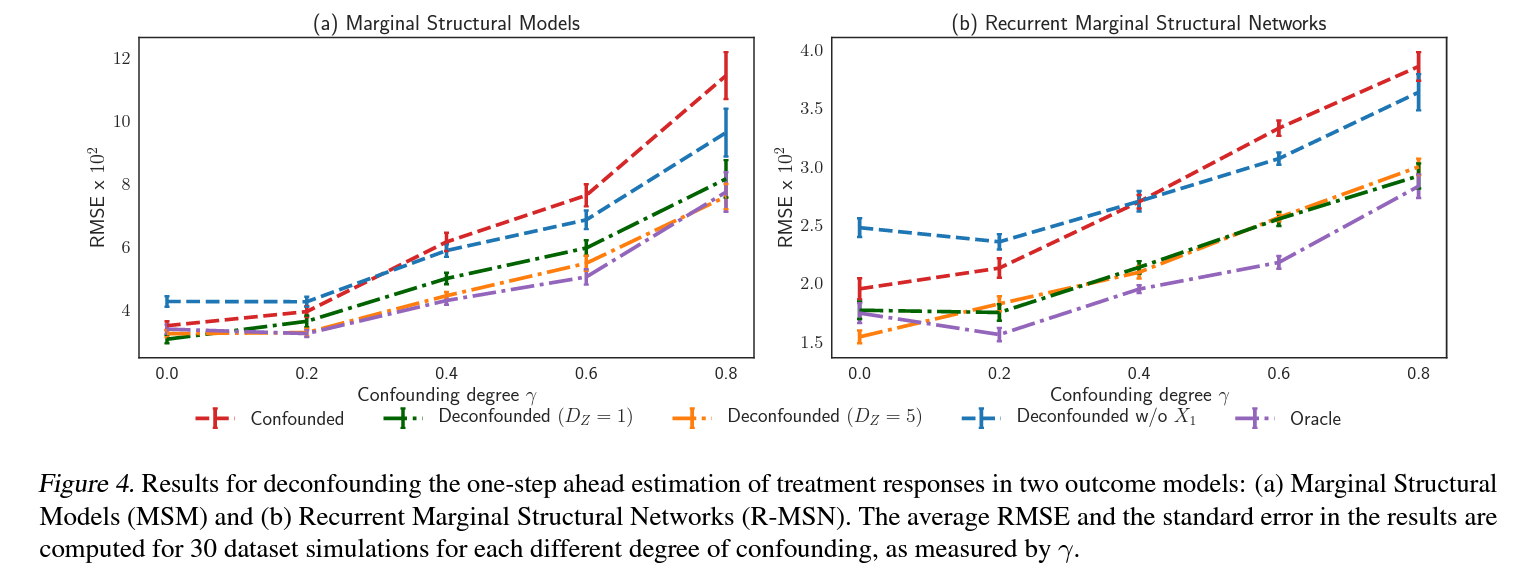
• 위 결과 그래프를 보면 Deconfounded에서 Confounded보다 Oracle과 유사한 결과를 보여주어 Time Series Deconfounder가 treatment response에 대해 unbiased estimation을 하는것을 확인함. 
• Deconfounded 두가지 경우, 서로 크게 차이나지 않는데서 hidden counfounder 크기에 대한 model misspecification과 관계없이 robust한 결과를 확인함.
• Single hidden confounder가 있을 경우엔 bias를 해결하지 못하는데서 Assumption3가 중요하단것을 확인함. 
• 5가지 경우 모두 RNN기반의 R-MSNs가 MSMs보다 뛰어난 정확성을 보여줌.

 

7. Experiments on MIMIC III

• Time Series Deconfounder를 실제 데이터에 대한 검증을 위해 EHR 오픈데이터인 MIMIC III의 6256명의 환자 데이터에 적용함.
• 특히 폐혈증 환자에서 항생제, 혈압상승제, 기계식 호흡장치의 총 3 가지의 treatment가 백혈구 개수, 혈압, 산소포화도의 각 3 가지 response에 어떻게 영향을 미치는지를 실험.
• 실제 데이터인만큼 폐혈증 외의 질병에 대한 cormorbidity나 몇 lab test가 기록에 없다던지의 hidden confounder가 존재하며, Oracle 경우를 확인 불가능함.

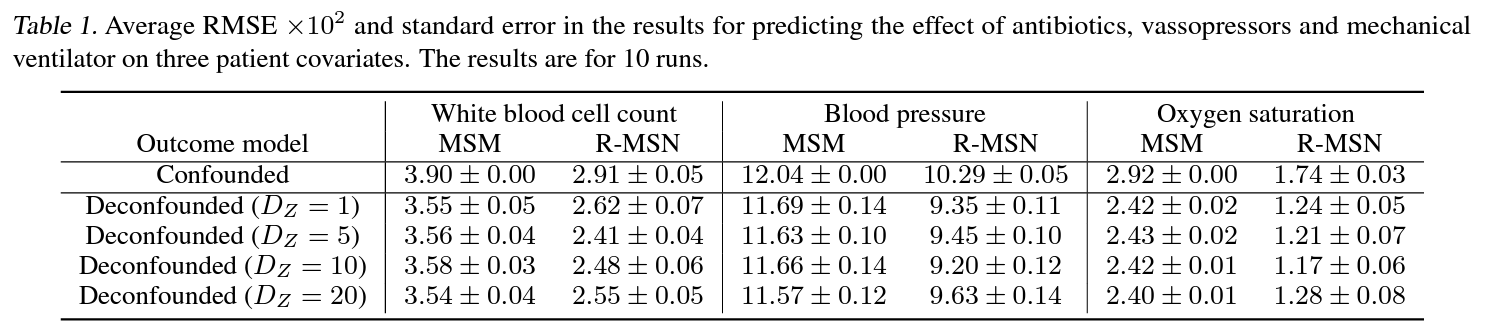
• 3 가지 response실험 모두에서 Confounded보다 Time Series Deconfounder를 적용할 경우 정확도가 상승하는것을 확임함.
• 합성데이터에서와 마찬가지로 RNN기반의 R-MSNs가 MSMs보다 뛰어난 정확성을 보여줌.
• 추후 의료진의 의견을 참고한 심층된 검증 필요.

 

8. Conclusion

• 관측된 시계열 환자 데이터에서 individualized treatment effect를 추론하는 기존 방법들에선 모두 hidden confounder가 없다는 가정을 했으나, 시계열 데이터에선 시간에 따라 환자의 상태가 계속 바뀌는데가 treatment를 결정하는 복잡도가 올라가 특히나 더 비현실적인 가정임.
• 이에 본 연구에선 hidden confounder를 대체가능한 latent variable을 추론하는 Time Series Deconfounder를 제안하고 RNN, multitask output, variational dropout을 사용하여 구현함.
• 합성데이터와 실제데이터를 사용하여 multi-cause hidden confounder가 있을때의 Time Series Deconfounder의 bias 제거 효과를 보여줌.

 

9. Appendix

• (Table 3.) Hidden confounder가 treatment와 outcome에 미치는 영향이 커질수록, 더 큰 capacity의 모델이 필요.
• (D.2) RNN기반의 treatment effect estimation이 시간에 따라 변화하는 treatment policy에 보다 robust.
• (Figure 6.) 실제 hidden confounder의 갯수와 같게 $D_Z$를 설정하거나 overestimate할 때 treatment response에 대한 예측도가 향상함.