Author :(Microsoft Research) Jiaqi Zhang, Joel Jennings, Cheng Zhang, Chao Ma
Paper Link: https://arxiv.org/abs/2310.00809

Author :(Google DeepMind) Andrew Kyle Lampinen, Stephanie C Y Chan, Ishita Dasgupta, Andrew J Nam, Jane X Wang
Paper Link: https://arxiv.org/abs/2305.16183
Talk1: https://www.youtube.com/watch?v=XkPv9bk4O3I (http://lxmls.it.pt/2023/slides/andrew.pdf)
Talk2: https://www.youtube.com/watch?v=3Go7yF5n62c

Author :(Microsoft) Cheng Zhang, Stefan Bauer, Paul Bennett, Jiangfeng Gao, Wenbo Gong, Agrin Hilmkil, Joel Jennings, Chao Ma, Tom Minka, Nick Pawlowski, James Vaughan
Paper Link: https://arxiv.org/abs/2304.05524

Author : Matej Zečević, Moritz Willig, Devendra Singh Dhami, Kristian Kersting
Paper Link: https://arxiv.org/abs/2301.12292

Code: https://github.com/moritzwillig/causalparrots

TMLR presentation: https://www.youtube.com/watch?v=vbwrhbuvedE 

Author : Hamed Nilforoshan, Michael Moor, Yusuf Roohani, Yining Chen, Anja Šurina, Michihiro Yasunaga, Sara Oblak, Jure Leskovec
Paper Link: https://arxiv.org/abs/2301.12292

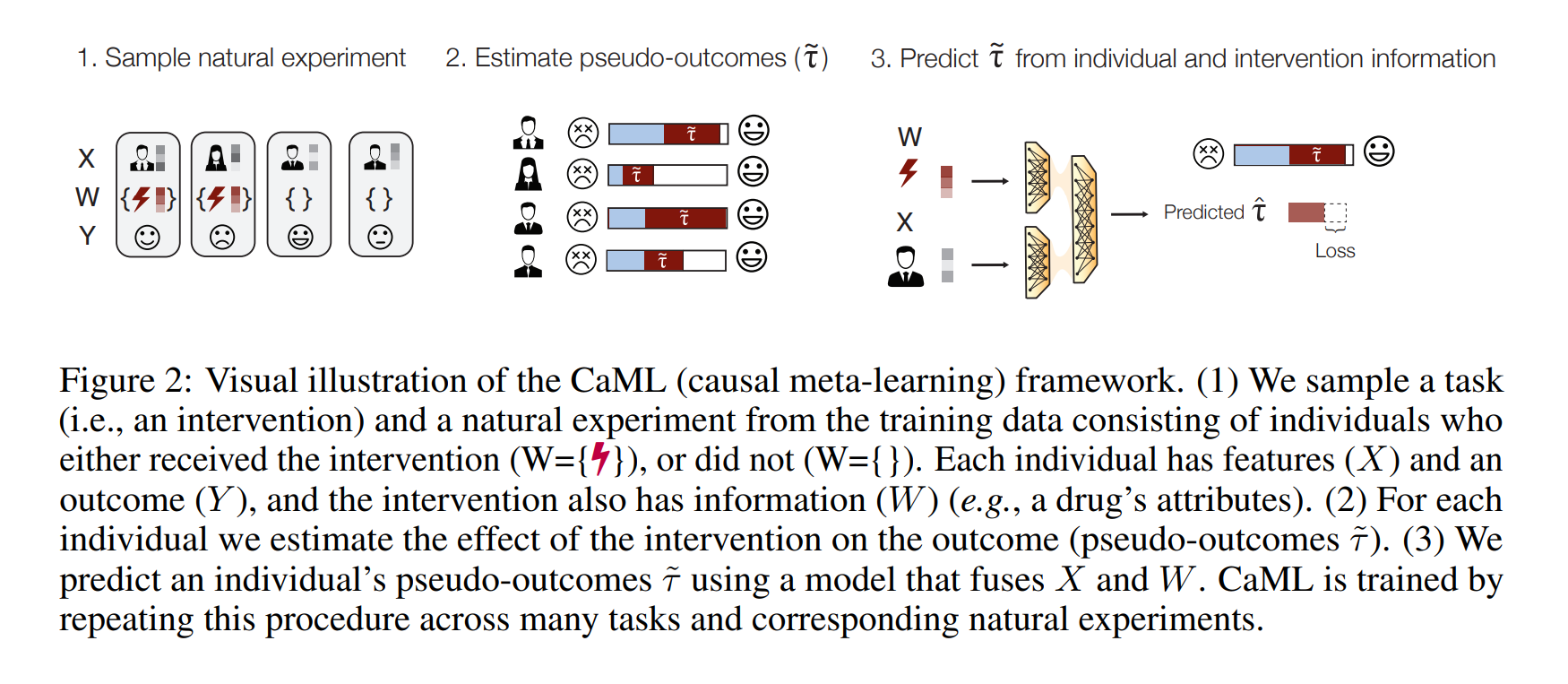
Author : Ahmed Alaa, Zaid Ahmad, Mark van der Laan
Paper Link: https://arxiv.org/abs/2308.14895

Github: https://github.com/AlaaLab/conformal-metalearners

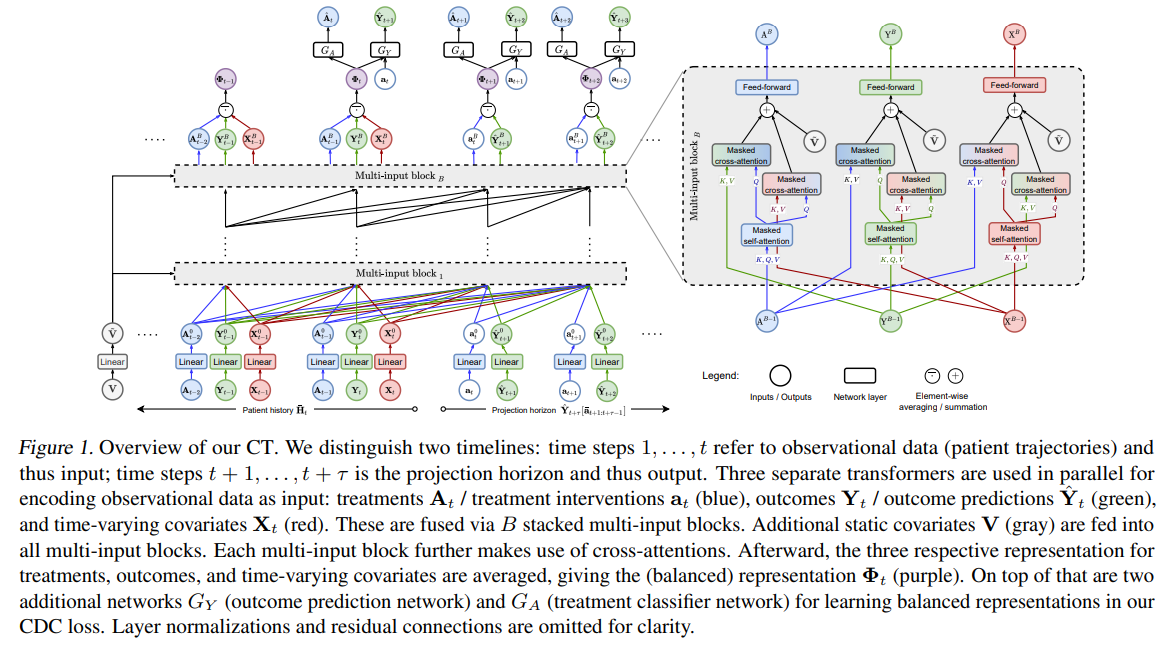
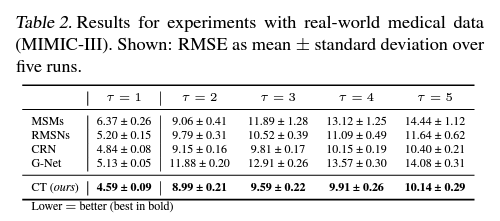
Author: Valentyn Melnychuk, Dennis Frauen, Stefan Feuerriegel
Paper Link: https://arxiv.org/abs/2204.07258

Code: https://github.com/Valentyn1997/CausalTransformer

ICML slide: https://icml.cc/media/icml-2022/Slides/17693.pdf

ICML presentation: https://slideslive.ch/38983812/causal-transformer-for-estimating-counterfactual-outcomes?ref=recommended 

• Time-varying confounder를 다루기 위해 CRN에서 LSTM을 사용한것과 달리 여기선 Transformer사용하여 길고 복잡한 sequence 데이터를 더 잘 다루고자 함
  • 저자 피셜 Transformer를 causal inference에 최초로 적용한 사례
• selection bias를 줄이기 위해 representation을 balancing 하는 접근을 택했고, 그 방법으로는 CRN과 같은 adversarial objectjve를 사용했으나 loss로는 doimain confusion loss를 사용했다는 차이첨이 있음
  • CRN의 방식은 학습속도 파라메터에 민감하기 때문에 자신들의 접근이 더 낫다 설명하고 실험으로 검증

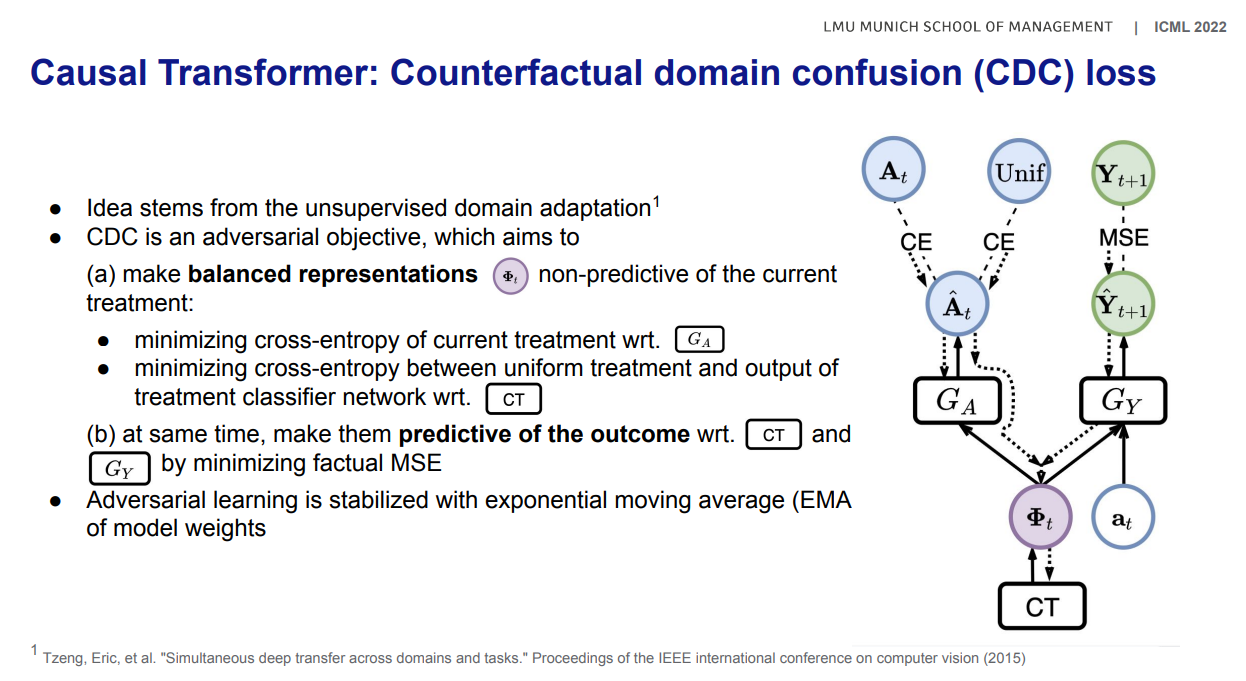
[Domain confusion loss]

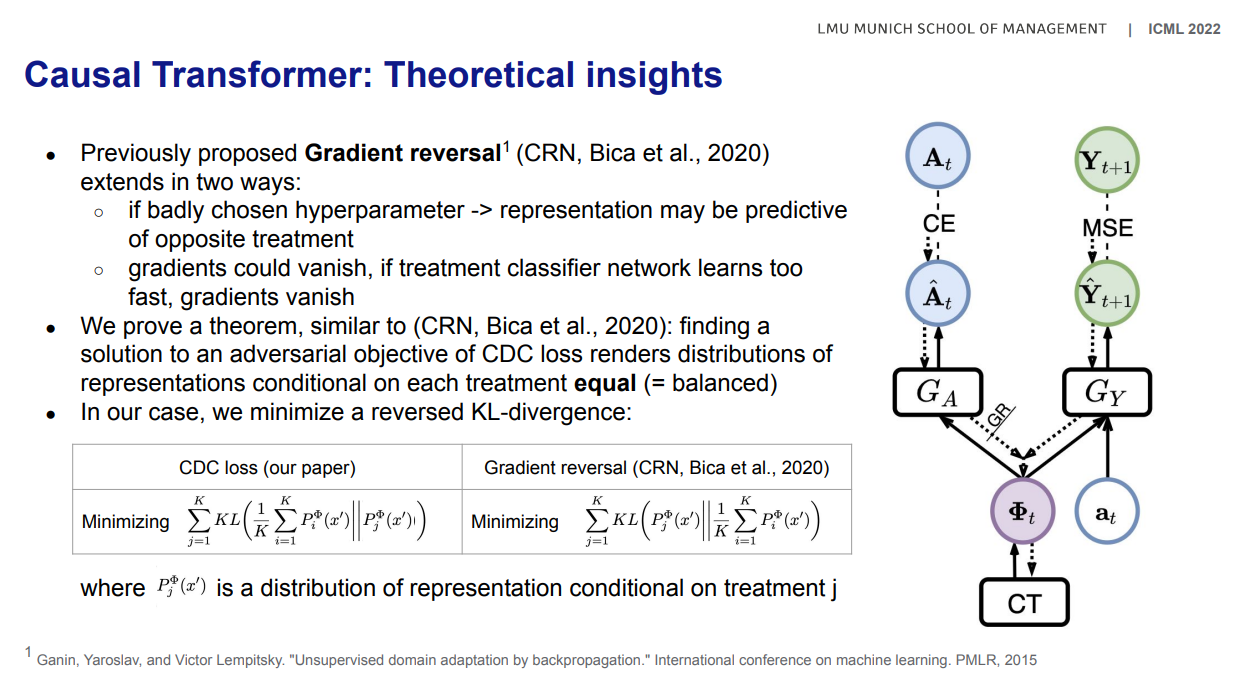
[Gradient reversal]

• 실험 결과 time dependent confounder 및 long term prediction 모두에서 기존 방법들 대비 높은 counterfactual 정확성을 보여줌

Author : Pedro A. Ortega, Markus Kunesch, Grégoire Delétang, Tim Genewein, Jordi Grau Moya, Joel Veness, Jonas Buchli, Jonas Degrave, Bilal Piot, Julien Perolat, Tom Everitt, Corentin Tallec, Emilio Parisotto, Tom Erez, Yutian Chen, Scott Reed, Marcus Hutter, Nando de Freitas, Shane Legg
Paper Link : https://arxiv.org/abs/2110.10819

• Sequential interaction에 대한 모델을 만들 땐, 단순 prediction loss만으론 self-delusion이 생기는 문제에 대한 DeepMind의 article.
• Delusion 문제를 다루기 위해 sequential 모델의 observation 분포와 action분포는 분리하여 학습해야하며, action의 probability에 대해선 intervention을 모델링하는 'counterfactual teaching'을 해야 delusion을 해소할 수 있다고 설명.
• 이 sequential 모델은 $\mathrm{RL}^2$와 같은 memory-based meta learning으로 학습이 가능함.
• 하지만 중요한 점은 위 설명은 online interaction이 가능한 경우에 대한것이고, offline learning의 경우 아직 open problem임을 설명.

개인적인 생각

• 주 저자들이 Deepmind Safety Analysis이다.
• 익히 알려진 'causal inference' 문제를 foundation model을 지향하는 관점에서 officially 정리해주었다.
• Offline learning에선 unobserved confounder가 있을 땐, observation 또한 단순 'factual teaching'기반의 prediction 문제로 학습할 경우 selection bias에 의한 delusion이 생기므로 주의해야한다.

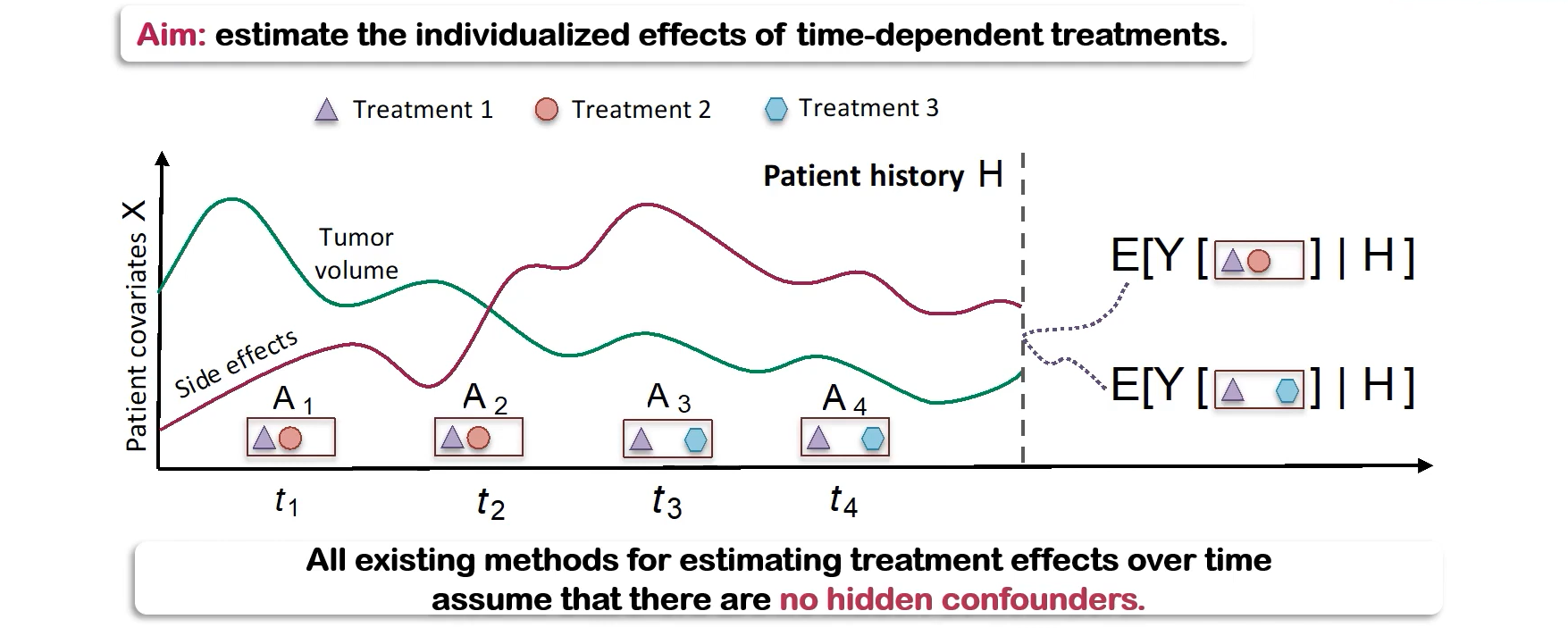
Author: Ioana Bica, Ahmed M Alaa, Mihaela van der Schaar
Paper Link: https://arxiv.org/abs/1902.00450

Talk in ICML2020: https://icml.cc/virtual/2020/poster/6131

Talk in van der Schaar Lab's Yutube Channel:  https://www.youtube.com/watch?v=TNPce1zd6rE 

Code: https://github.com/ioanabica/Time-Series-Deconfounder

0. Abstract

• 의료분야에서 treatment effect를 추론하는것은 중요하지만, 지금까지의 추론 방법들은 모두 'no hidden confounder'라는 비현실적이고 결과적으로 추론에 bias를 야기하는 가정을 전제로 함.
• 본 연구에서는 시간에 따른 다중 치료 환경에서 multi-cause hidden confounder가 존재할때의 treatment effect를 추론하기위한 Time Series Deconfounder를 제안함.
• Time series Decounfounder는 multitask output의 RNN을 factor model로 사용하여 multi-cause unobserved confounder를 대체하는 latent variable을 추론하고 이를통해 casual inference를 수행함.  
• 이론적 분석과 함께 시뮬레이션 및 실제 MIMIC III데이터를 사용하여 알고리즘의 효과성을 검증함.

1. Introduction

• 연속적으로 처방된 치료에 따른 환자 개인의 치료 효과를 예측하는것은 매우 중요한 문제임.
• 최근 이러한 정보를 담고있는 observational 데이터 역시 빠르게 증가하고 있음.
• 하지만 기존의 방법들은 모든 confounder가 관측가능하다는 대체로 비현실적인 상황을 가정하고있어 예측에 bias가 생김.
• 예를들어 암의 진행에대한 항암제의 효과를 예측할 때 환자의 약에대한 내성형성이나 누적되는 독성을 고려하지 않는것은 예측결과에 bias를 초래.
• 하지만 내성이나 독성은 관측이 어렵고 관측이 되더라고 후향적인 EHR과 같은 후향적인 관측데이터에는 기록되어있지 않은 경우가 대부분.
• 본 연구에선 Wang & Blei (2019a)의 연구에서 고안된 'static 셋팅에서의 multiple treatment를 활용하여 hidden confounder를 deconfounding하는 방법'을 개선하여 longitudinal 셋팅에서의 time-varying hidden confounder를 deconfounding하는 Time Series Deconfounder를 제안함.
• 시계열 환경에서 unobserved confounder의 대체재로서 letent variable을 학습하는 첫번째 시도.

2. Related Work

• 시간에 따라 변하는 치료에 대한 Potential outcomes
  - 지금까지 시계열 데이터에 대한 counterfacutal inference로는 G-formula, G-estimation, MSM, R-MSN, balaced representation 등이 있었지만 모두 hidden confounder가 없다고 가정.
  - 연속성 데이터에대한 treatment effect 연구들도 있어왔으나 여기선 이산 환경을 다룸.
  - Unmeasured confounder에 대한 potential impact를 평가하기위한 sensitivity anlysis방법들도 고안되어옴.
• Hidden confounder 추론을 위한 latent variable 모델
  - Multi-cause 환경에서 hidden confounder를 추론가능한 latent variable로 대체하고 추론된 latent variable로 causal inference를 수행하는식의 deconfounder 접근은  Wang & Blei (2019a, link)에서 제안된 바 있음.
  - 해당 논문은 static treatment 문제를 다루고 있으나, 본 논문은 이와 달리 time-varying treatment문제를 다루기 위해 RNN을 factor model로 사용하는 deconfounder 구조를 제안함. 

3. Problem Formulation

• $\mathbf{X}_{t}^{(i)} \in \mathcal{X}_{t}$: random variable, (환자 $i$에 대한; 이후 생략) time-dependent covariates
• $\mathbf{A}_{t}^{(i)}=\left[A_{t1}^{(i)}{\cdots}A_{tk}^{(i)}\right]\in\mathcal{A}_{t}$: 시간 $t$에서의 가능한 $k$가지 treatments
• $\mathbf{Y}_{t+1}^{(i)}\in\mathcal{Y}_{t}$: 관측된 outcomes
• $\tau^{(i)}=\left\{{\mathbf{x}_t^{(i)}},{\mathbf{a}_t^{(i)}},{\mathbf{y}_{t+1}^{(i)}}\right\}_{t=1}^{T^{(i)}}$: 이산시간 $T^{(i)}$ 동안 수집된 trajectory 샘플
• $\mathcal{D}=\left\{{\tau^{(i)}}\right\}_{i=1}^{N}$: $N$명의 환자에 대한 EHR 데이터
• $\overline{\mathbf{A}}_t=(\mathbf{A}_1,\cdots,\mathbf{A}_t)\in\overline{\mathcal{A}}_t$: 시간 $t$까지의 treatment history
• $\overline{\mathbf{X}}_t=(\mathbf{X}_1,\cdots,\mathbf{X}_t)\in\overline{\mathcal{X}}_t$: 시간 $t$까지의 covariates history
• $\mathbf{Y}(\overline{a})$: 가능한 treatment course $\overline{a}$에 대한 potential outcome (factual & counterfactual)
• 아래의 Individualized treatment effect (ITE), 즉 환자 개인의 covariate history와 treatment history가 주어졌을때의 potential outcome, 을 추론하는것이 이 연구의 목표

$\mathbb{E}[\mathbf{Y}(\overline{a}_{\geq{t}}){\vert}\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]$

• 아래 세 가지 가정 하에서는 bias가 생기지 않아 위 potential outcome에 대한 추론은 우항의 관측된 outcome에 대한 regression과 동치

 $\mathbb{E}[\mathbf{Y}(\overline{a}_{\geq{t}}){\vert}\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]=\mathbb{E}[\mathbf{Y}{\vert}\overline{a}_{\geq{t}},\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]$

  Assumption 1. Consistency

  Assumption 2. Positivity (Overlap)

  Assumption 3. Sequencial strong ignorability (no hidden confounders)

$\mathbf{Y}(\overline{a}_{\geq{t}}){\perp\!\!\!\!\perp}\mathbf{A}_t\vert\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_{t}$

• 하지만 세번째 가정은 좌변의 counterfactual로 인해 테스트가 불가능하며 현실적이지 않아 여기서는 hidden confounder가 있는 보다 현실적인 문제를 다루고자 함.
• 따라서 위에서 언급한 동치는 성립하지 않음.

$\mathbb{E}[\mathbf{Y}(\overline{a}_{\geq{t}}){\vert}\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]\neq \mathbb{E}[\mathbf{Y}{\vert}\overline{a}_{\geq{t}},\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]$

• 대신 Wang & Blei (2019a)의 접근을 확장하여 시간에 따른 다중 treatments를 활용한 sequencial latent variable $\overline{\mathbf{Z}}_t=(\mathbf{Z}_1,\cdots,\mathbf{Z}_t)\in\overline{\mathcal{Z}}_t$ 을 추론하고 관측되지 않은 confounders로서 대체하고자 함.

4. Time Serise Deconfounder

• 본 연구에서 제안하는 Time Series Deconfounder의 본질적인 아이디어는 multi-cause confounder로 인한 treatment들 사이의 종속성이 있다는것.
• 이 종속성을 활용하여 시간에 따라 바뀌는 treatment로 부터 hidden confounder를 추론함.

4.1. Factor Model

• Time Series Deconfounder는 시간 $t$이전까지의 history $\overline{\mathbf{h}}_{t-1}$로부터 시간 $t$에서의 unobserved confounder를 대체할  letent variable $z_t$을 추론하는 factor model $g$을 가짐.

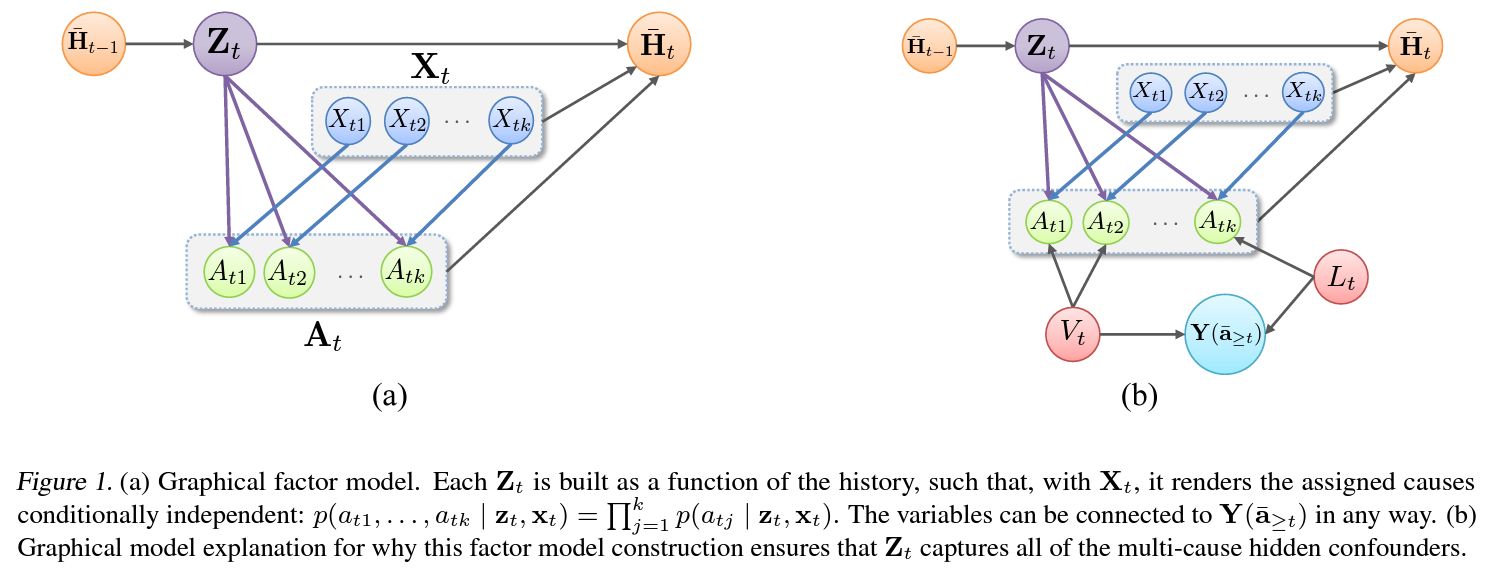
$\mathbf{z}_t=g(\overline{\mathbf{h}}_{t-1})$

,where  $\overline{\mathbf{h}}_{t-1}=(\overline{\mathbf{a}}_{t-1},\overline{\mathbf{x}}_{t-1},\overline{\mathbf{z}}_{t-1})$

• 이를 그래프로 나타내면 위 그림$(a)$와 같으며, latent variable  $\mathbf{z}_t$는 시간 $t$에서의 treatment들에 대한 multi-cause unobserved confounder를 대체하는 역할로서 나타낼 수 있음. 
• Multi-cause unobserved confounder로 인한 treatment들 사이의 종속성으로 인해 factor model을 사용하여 latent variable의 sequence $\overline{\mathbf{Z}}_t$를 추론 할 수 있음.
• 이때, latent variable $\mathbf{Z}_t$는 모든 multi-cause confounder를 내포하고 있음을 보장 (treatment사이의 종속성을 활용한 귀류법).
• 즉, 위 그림$(b)$에서와 같이 또다른 multi-cause confounder $V_t$는 존재하지 않음.
• 하지만 $L_t$와 같은 single-cause confounder가 없는것은 보장할 수 없으므로 다음을 새롭게 가정하고, 위에서 언급한 기존 방법들에서 사용한 세가지 가정 중 세번째 가정을 대체.

  Assumption 3. Sequential single strong ignorability (no hidden single cause confounders)

$\mathbf{Y}(\overline{a}_{\geq{t}}){\perp\!\!\!\!\perp}{A}_{tj}\vert\mathbf{X}_{t},\overline{\mathbf{H}}_{t-1}$

• 물론 이 가정 역시 여전히 테스트가 불가능하지만, 관측가능한 treatment의 갯수가 증가함에 따라 hidden confounder가 하나의 treatment에만 영향을 줄 가능성은 급격히 줄어듬.
• Wang & Blei (2019a)에 따르면 $\mathbf{Z}_t$의 차원이 treatments의 갯수보다 작을경우 가정2. Positivity또한 실질적으로 만족가능.
• Fitting된 factor model이 얼마나 정확하게 validation set 환자의 treatment분포를 예측하는지를 평가하기위해 predictive check로서 각 시간 $t$에서 $M$개의 예측 샘플과 실제treatment 사이의 $p$-value를 아래와 같이 계산.

$\frac{1}{M}\sum_{i=1}^{M}\mathbf{1}(T(a_{t,rep}^{i})<T(a_{t,val}))$

,where $T(a_t)=\mathbb{E}_z[\mathrm{log}\,p(a_t{\vert}Z_t,X_t)]$ is test statistic and $\mathbf{1(\cdot)}$ is indicator function

• Fitting이 잘 된 경우 $p$-value는 0.5에 가까움.

4.2. Outcome Model

• Factor model이 잘 fitting된 다음 스텝으로 Time Series Deconfounder는 아래의 좌변의 시간에 따른 individualized treatment effect를 추론하기위한 outcome model을 우변과 같이 fitting.

$\mathbb{E}[\mathbf{Y}(\overline{a}_{\geq{t}}){\vert}\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]=\mathbb{E}[\mathbf{Y}{\vert}\overline{a}_{\geq{t}},\overline{\mathbf{A}}_{t-1},\overline{\mathbf{X}}_t]$

• Time Series Deconfounder의 uncertainty는 factor model에서 시간에 따라 샘플된 sequential latent variable $\hat{\bar{\mathbf{Z}}}_t=(\hat{\mathbf{Z}}_1,\cdots,\hat{\mathbf{Z}}_t)$ 을 다시 반복 샘플하여 구한 각각의 outcome들의 variance로 판단함.
• 만약 treatment effect가 부정확하여 non-identifiable할 경우엔 이 variance가 커짐.
• 또한 본 연구에서 제안하는 hidden confounder문제를 다루기 위해 latent variable를 추론하는 접근은 treatment effect의 bias를 명백히 낮추지만, Wang & Blei (2019a)에 따르면 hidden confounder가 없는 상황에선 기존 방법 대비 variance가 상대적으로 커져 free lunch는 아님. 

5. Factor Model over Time in Practice

• 시계열 문제를 다루고 있으므로 기존의 PCA나 Deep Exponential Families을 사용하는 대신 아래 그림과 같이 RNN, 여기서는 특히 LSTM을 factor model로서 사용함.

• 즉, RNN을 사용하여 환자의 시간 $t$까지의 history로 부터 시간 $t$에서의 latent variable을 추론.

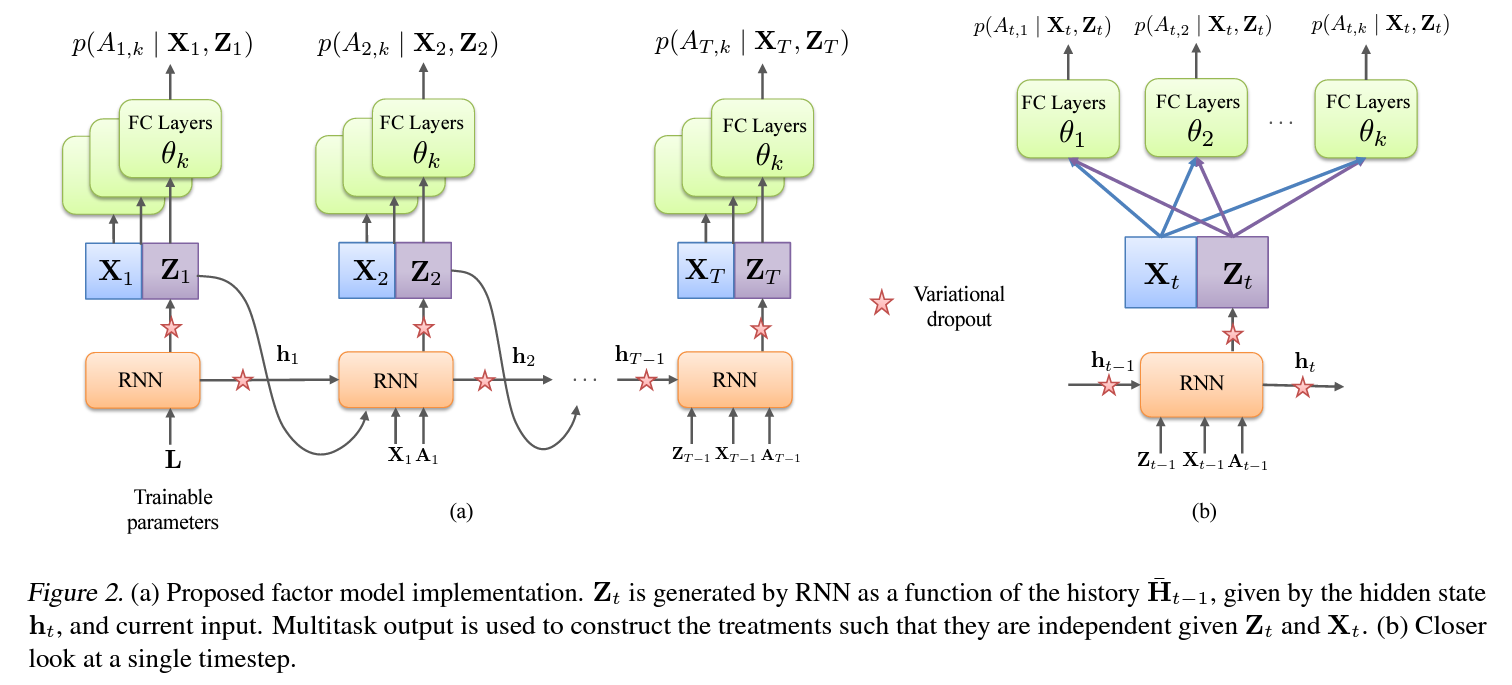
$\mathbf{Z}_1=\mathrm{RNN}(\mathbf{L})$

$\mathbf{Z}_t=\mathrm{RNN}(\overline{\mathbf{Z}}_{t-1},\overline{\mathbf{X}}_{t-1},\overline{\mathbf{A}}_{t-1},\mathbf{L})$

• RNN의 출력사이즈는 $D_Z$이며 $\mathbf{L}$은 학습가능한 initial paramter.
• RNN에서 추론된 Latent variables $\mathbf{Z}_t$와 관측된 covariates $\mathbf{X}_t$에 조건부 독립인 treatment $\mathbf{A}_t=[A_{t1},\cdots,A_{tk}]$를 추론하기위해서 treatment 개수 $k$만큼의 single FC MLP레이어를 RNN의 출력단에 multitask output으로 붙임.

$A_{tj}=\mathrm{FC}(\mathbf{X}_t, \mathbf{Z}_t;\theta_j)$

• Binary treatment의 경우엔 출력레이어에 sigmoid activation을 사용함.
• Factor model의 확률적인 특징을 구현하기위해서 위 그림의 별이 그려진 부분에 $variational\,dropout$(GAL & Ghahramani, 2016a)을 사용하였고, 이에 따른 latent variable의 샘플링이 가능해짐.
• 위와 같은 구현으로 RNN으로 하여금 $\overline{\mathbf{X}}_t$, $\overline{\mathbf{Z}}_t$ 및 $\overline{\mathbf{A}}_t$사이의 복잡환 관계를 학습도록 할 수 있지만, 이 과정에서 predictive check가 반드시 필요하다는것에 주의.

6. Experiments on Synthetic Data

• 제안한 Time Series Deconfounder를 검증하고자 합성데이터를 사용함.
• 실제 데이터를 사용한 검증은 hidden confounder를 알 수 없으므로 불가능.

6.1. Simulated Dataset

• 5000명의 환자에 대한 20~30 스텝의 가상데이터를 treatments, covariates, hidden confounders가 서로 영향을 미치는 $p$-order autoregressive 과정으로 생성함 (자세한 수식은 논문 참조).
• 그리고 outcome은 covariates와 hidden confounder의 함수가 되도록 생성.

6.2. Evaluating Factor Model using Predictive Checks

• 제안한 factor model 아키텍처가 treatment의 분포를 잘 학습하는지 확인하고자 합성데이터에 대해 아래 세 가지 모델의 predictive check를 수행함.
  1. 제안한 factor model; RNN + Multitask FC output (초록)
  2. RNN대신 MLP를 사용한 factor model (파랑)
  3. Multitask FC layer대신 단일 FC layer를 사용한 factor model (보라)

• 실험 결과 RNN대신 MLP를 사용할 경우 시간이 지남에 따라 지속적인 distribution mismatch가 생김.
• Multitask output은 treatment distribution을 파악하는데 도움은 되나 큰 영향을 주는것은 아님을 확인.
• 즉, factor model에 RNN아키텍처를 사용하는것이 hidden confounder의 시간 의존적인 특성을 캡쳐하는데 있어 중요하며, 현재 스텝의 covariates와 confounders가 잘 명시될 경우 treatment distribution을 학습할 수 있다고 결론.

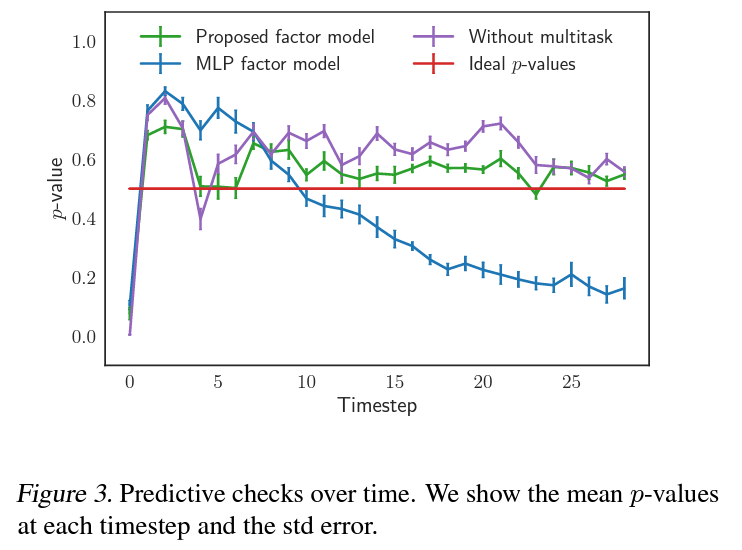
6.3. Deconfounding the Estimation of Treatment Responses over Time

• Time Series Deconfounder가 confounder에 의한 bias를 잘 deconfounding하는지를 다음의 두 outcome model을 사용하여 검증함. 

1. Standard Marginal Structural Models (MSMs)
   - Logistic regression으로 구한 inverse probability of treatment weighting(IPTW)을 사용하여 confounder가 balance된 pseudo-population을 생성하는 단계와, 이렇게 생성된 pseudo-population으로부터 treatment reponse를 linear regression하는 단계의 두 가지 스텝으로 구성된 selection bias 대응방법.
   - 이름에서 'marginal'은 counfounder control의 의미이며, 'structural'은 potential outcome framework를 의미함.
   - MSMs에 대한 자세한 내용은 다음 두 강의를 참고
   (https://www.youtube.com/watch?v=7NjIQTzADgQ)
   (https://www.coursera.org/lecture/crash-course-in-causality/marginal-structural-models-EUpei)
2. Recurrent Marginal Structural Networks (R-MSNs; Lim et al., 2018)
   - MSMs와 접근은 같지만 RNN을 사용하여 propensity score를 추론하고 treatment response 역시 RNN을 사용하여 추론하는것이 차이.
   - $\mathrm{RNN}(\overline{\mathbf{X}}_t,\overline{\mathbf{Z}}_t,\overline{\mathbf{A}}_t)$ 와 같이 구현하며, RNN을 사용하여 추정한 propensity weights에 따라 weight를 각 환자에 주어 loss함수를 계산.

• 평가를 위해 한 스텝 다음의 treatment response를 예측하는 테스크를 사용하였으며, 두 outcome model에 대한 자세한 분석을 위해 아래 5가지 경우를 비교
  1) Confounded: hidden confounder를 고려하지 않고 관측데이터를 그대로 사용한 경우. 
  2) Deconfounded ($D_z=1$): 실제 hidden confounder의 크기인 1과 동일한 크기의 latent variable $\hat{\overline{\mathbf{Z}}}_t$를 사용한 경우.
  3) Deconfounded ($D_z=5$): 실제 hidden confounder의 크기인 1과 다른, 크기 5의 latent variable $\hat{\overline{\mathbf{Z}}}_t$를 사용한 경우.
  4) Deconfounded w/o $X_1$: Assumption 3를 위반한 경우로 single cause confounder $X_1$를 covariate에서 제거하여 hidden confounder로 가정한 경우.
  5) Oracle: 합성데이터에서의 실제 ground truth hidden confounder $\overline{\mathbf{Z}}_t$를 outcome 모델에 넣어준 경우. 

• 위 결과 그래프를 보면 Deconfounded에서 Confounded보다 Oracle과 유사한 결과를 보여주어 Time Series Deconfounder가 treatment response에 대해 unbiased estimation을 하는것을 확인함. 
• Deconfounded 두가지 경우, 서로 크게 차이나지 않는데서 hidden counfounder 크기에 대한 model misspecification과 관계없이 robust한 결과를 확인함.
• Single hidden confounder가 있을 경우엔 bias를 해결하지 못하는데서 Assumption3가 중요하단것을 확인함. 
• 5가지 경우 모두 RNN기반의 R-MSNs가 MSMs보다 뛰어난 정확성을 보여줌.

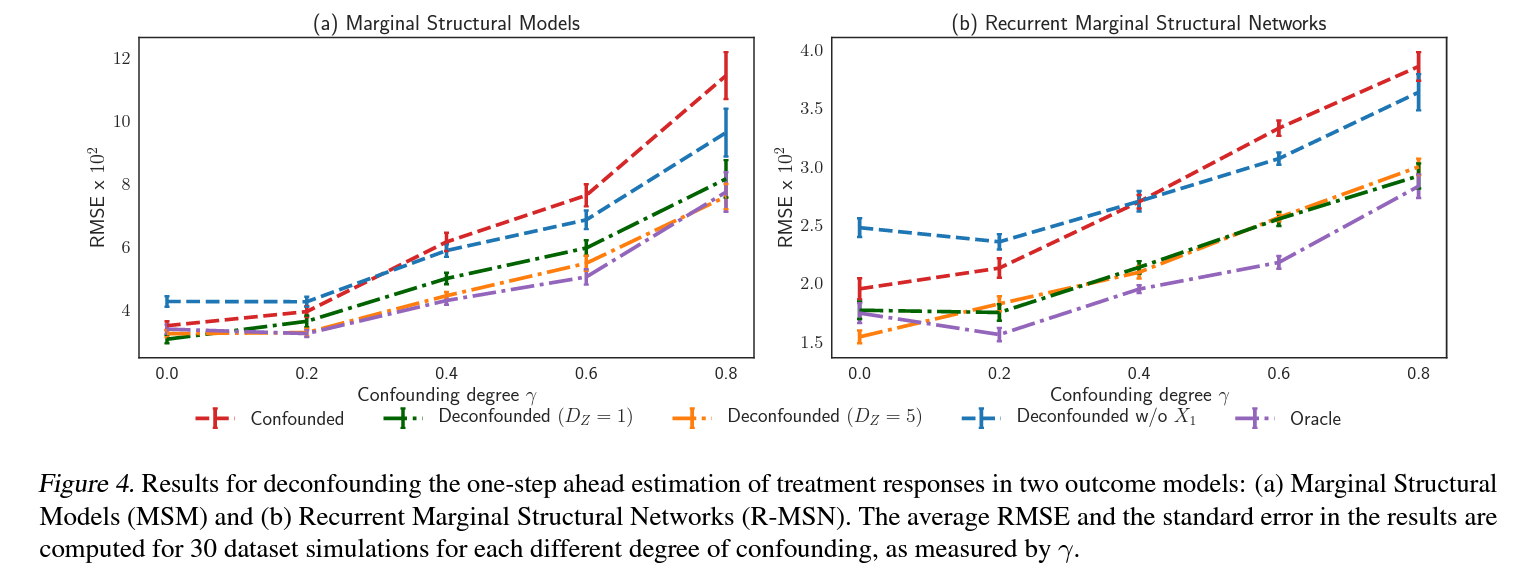
7. Experiments on MIMIC III

• Time Series Deconfounder를 실제 데이터에 대한 검증을 위해 EHR 오픈데이터인 MIMIC III의 6256명의 환자 데이터에 적용함.
• 특히 폐혈증 환자에서 항생제, 혈압상승제, 기계식 호흡장치의 총 3 가지의 treatment가 백혈구 개수, 혈압, 산소포화도의 각 3 가지 response에 어떻게 영향을 미치는지를 실험.
• 실제 데이터인만큼 폐혈증 외의 질병에 대한 cormorbidity나 몇 lab test가 기록에 없다던지의 hidden confounder가 존재하며, Oracle 경우를 확인 불가능함.

• 3 가지 response실험 모두에서 Confounded보다 Time Series Deconfounder를 적용할 경우 정확도가 상승하는것을 확임함.
• 합성데이터에서와 마찬가지로 RNN기반의 R-MSNs가 MSMs보다 뛰어난 정확성을 보여줌.
• 추후 의료진의 의견을 참고한 심층된 검증 필요.

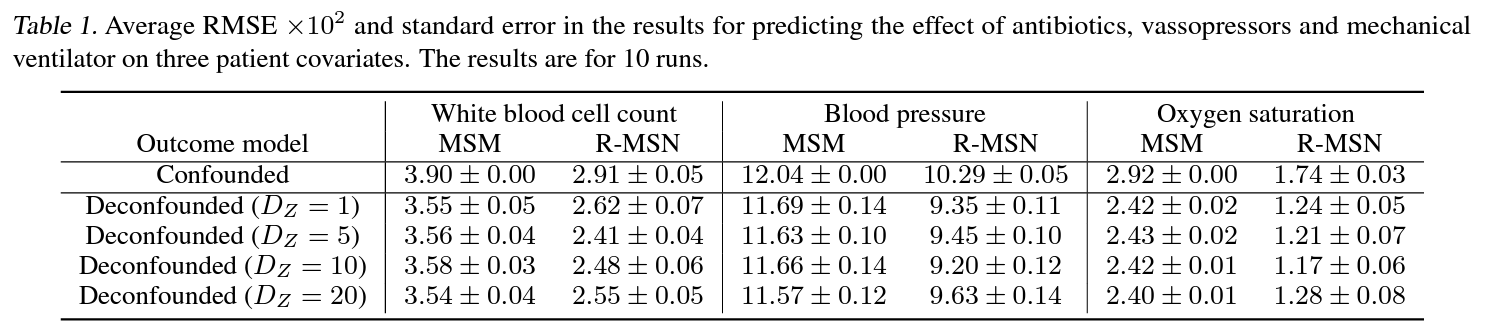
8. Conclusion

• 관측된 시계열 환자 데이터에서 individualized treatment effect를 추론하는 기존 방법들에선 모두 hidden confounder가 없다는 가정을 했으나, 시계열 데이터에선 시간에 따라 환자의 상태가 계속 바뀌는데가 treatment를 결정하는 복잡도가 올라가 특히나 더 비현실적인 가정임.
• 이에 본 연구에선 hidden confounder를 대체가능한 latent variable을 추론하는 Time Series Deconfounder를 제안하고 RNN, multitask output, variational dropout을 사용하여 구현함.
• 합성데이터와 실제데이터를 사용하여 multi-cause hidden confounder가 있을때의 Time Series Deconfounder의 bias 제거 효과를 보여줌.

9. Appendix

• (Table 3.) Hidden confounder가 treatment와 outcome에 미치는 영향이 커질수록, 더 큰 capacity의 모델이 필요.
• (D.2) RNN기반의 treatment effect estimation이 시간에 따라 변화하는 treatment policy에 보다 robust.
• (Figure 6.) 실제 hidden confounder의 갯수와 같게 $D_Z$를 설정하거나 overestimate할 때 treatment response에 대한 예측도가 향상함.

Author: Ioana Bica, Daniel Jarrett, Alihan Hüyük, Mihaela van der Schaar
Paper Link: https://openreview.net/forum?id=h0de3QWtGG 

Talk in ICLR2021: https://iclr.cc/virtual_2020/poster_BJg866NFvB.html

Rating: 8, 7, 6, 5

Author  : Yaobin Ling, Pulakesh Upadhyaya, Luyao Chen, Xiaoqian Jiang, Yejin Kim
Paper Link : https://arxiv.org/abs/2109.12769

박지용 교수님께서 기획하신 2021년 인과추론 써머세션에서 김예진 교수님께서 강의해주신 Heterogenous Treatment Effect Estimation using ML 세션을 정말 재밌게 들었는데, 이에 대한 튜토리얼 및 벤치마크 논문이 워킹페이퍼로 공개되었다. 논문을 보면 필요한 용어에 대해 상세히 정의해두었고 특히 예시를 정말 잘 활용하고 있어서 처음 causal inference를 접하는 사람들에게 너무 좋은 내용이다.

아래는 줌으로 실강을 듣고나서도 여러번 반복해서 더 들은 김예진 교수님의 강의.  이런 좋은 강의를 한국어로 들을 수 있다니 두 교수님께 감사하다. 

Author  : Andrew Forney, Elias Bareinboim
Paper Link : https://ojs.aaai.org//index.php/AAAI/article/view/4090

Author  : Ioana Bica, Ahmed M Alaa, James Jordon, Mihaela van der Schaar
Paper Link : https://openreview.net/forum?id=BJg866NFvB 

Talk in ICLR2020: https://iclr.cc/virtual_2020/poster_BJg866NFvB.html

Rating: 8, 6, 6

Author  : Anonymous (Naver Labs Europe이지 않을까)
Paper Link : https://openreview.net/forum?id=1L0C5ROtFp

Rating: 5, 6, 10

Author : Anonymous authors
Paper Link : https://openreview.net/forum?id=uy602F8cTrh 

• Model-based RL에 structural causal inference을 적용하여 OOD에서의 generalization을 향상시키고자 함

• 동일한 환경의 방문한 transition을 시작점으로 data를 생성해 data augmentation을 시도하는 기존 Dyna 타입의 알고리즘과 달리 counterfactual data를 world model로 생성
• 이때 로봇이 옮기고자 하는 물건의 질량 혹은 마찰력에 대한 structual causal model을 가정하고 이를 counterfauctual peroperty로 설정

• 실험은 robot manipulation task에대한 transfer learning을 검증하기위해 개발된 환경인 CausalWorld에서 진행
  - https://sites.google.com/view/causal-world/home (Youshua Bengio 교수님 포함)
• 질량과 마찰력에 대한 OOD 조건에서 실험결과 기존 model-based RL 및 model-free RL 알고리즘 (MBPO & SAC)보다 더 나은 task generalization 및 sample efficeincy를 보여줌

• 또한 학습조건의 질량과 마찰력이 한쪽으로 쏠린 unbalanced distribution (90:5:5)에서도 다른 알고리즘 대비 더 나은 generalization 및 sample efficient한 성능을 보여줌 

개인적인 생각

• model-based RL이 real world에서 쓰이기위해 꼭 필요하다고 생각했던, 그리고 causal inferece의 인기를 생각하면 조만간 나올거라 생각했던 counterfactual performance를 다룬 연구라 반가웠다.
• 다만 다른 몇몇 casual inference연구의 결과에서도 그랬지만, 이 연구도 모델에 counterfactual property에 대한 loss가 따로 들어가지 않는 경우라 생성된 counterfactual data에 대한 신뢰성이 사실상 없다. (21.11.09 코멘트: 그래서인가 오늘 공개된 openrewiew에서 5353점을 받았다.)
• Structured casual graph를 쓰는만큼 앞으로는 더욱 inductive bias를 잘 활용할 수 있는 방향으로, 그래서 학습된 world model이 실제 환경의 dynamics에 대한 근본적인 이해를 바탕으로 만든 causal inference가 접목되지 않을까 싶다.
• 이 논문은 multi-task RL과 그 연장선으로 볼 수 있는데, meta-learning에도 causal inference를 접목하는 연구가 general intelligence를 최종 목표로하는 분야의 특성상 곧 나올것 같다. 

Author : Amir Feder, Katherine A. Keith, Emaad Manzoor, Reid Pryzant, Dhanya Sridhar, Zach Wood-Doughty, Jacob Eisenstein, Justin Grimmer, Roi Reichart, Margaret E. Roberts, Brandon M. Stewart, Victor Veitch, Diyi Yang
Paper Link : https://arxiv.org/abs/2109.00725

Related Repository: https://github.com/causaltext/causal-text-papers